9. 身近なデータで学ぶ統計の基本

前回はデータの可視化について学びました。今回は、データを数値的に分析する統計の基礎を学んでいきましょう。

9.1 統計とは？クラスの平均点や身長のばらつきを例に考える
9.2 平均・中央値・最頻値でデータの「中心」をつかむ
9.3 四分位数と箱ひげ図でデータの広がりを見てみる（成績分布など）
9.4 分散・標準偏差を使ってデータのばらつきを数値化する
9.5 散布図で 2 つのデータの関係を調べよう（勉強時間とテスト点数）
9.6 相関係数で「強い関係」か「弱い関係」か判断する
9.7 回帰直線で「未来」を予測してみる（勉強時間から点数を予測）
Ex.1 クラス全員の身長データから平均・中央値・標準偏差を計算して特徴をまとめる
Ex.2 勉強時間とテスト点数のデータで散布図を描き、相関係数や回帰直線を求めて関係を考える

9.1 統計とは？クラスの平均点や身長のばらつきを例に考える

統計とは、大量のデータを収集し、整理・分析することで、そのデータの持つ特徴や傾向を数値や図表で表す方法です。統計を学ぶとデータに基づいた判断ができるようになります。感覚や印象だけでなく、実際のデータを分析することで、より客観的で正確な判断の助けになります。

統計で何がわかるのか

中心傾向の把握：平均値や中央値で、データの「中心」がどこにあるかが分かる
散らばり具合の把握：範囲や標準偏差で、データのばらつき具合が分かる
分布の形状の把握：ヒストグラムで、データがどのように分布しているかの形状が分かる
外れ値の発見：他のデータから大きく離れた値（外れ値）を見つけることができる
データ間の関連性の分析：複数のデータ間に関連性があるかどうかを調べることができる

このように、数値計算やデータの可視化を使うことで、データから様々な情報を引き出すことができます。

NumPy で統計計算をする

Python では、NumPy というライブラリを使うことで、簡単に統計計算ができます。Numpy は、科学計算のための Python のライブラリです。

Google Colab では最初からインストールされているため、そのまま使うことができます！

以下のような関数を使うことで、簡単に統計計算ができます。

関数	説明	使用例
`np.mean()`	平均値を計算する	`np.mean(heights)`
`np.median()`	中央値を計算する	`np.median(heights)`
`np.max()`	最大値を求める	`np.max(heights)`
`np.min()`	最小値を求める	`np.min(heights)`
`np.std()`	標準偏差を計算する	`np.std(heights)`
`np.var()`	分散を計算する	`np.var(heights)`

身近な例で統計を考えてみよう

例えば、クラスの生徒の身長データを見てみましょう。このデータから何が分かるでしょうか？

クラスの身長データ例

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# クラスの身長データ例 （cm）
heights = [165, 172, 168, 170, 175, 163, 169, 167, 173, 166]

# 基本的な統計量の計算
mean_height = np.mean(heights)     # 平均
max_height = np.max(heights)       # 最大値
min_height = np.min(heights)       # 最小値
range_height = max_height - min_height  # 範囲（最大と最小の差）

print(f"平均身長：{mean_height:.1f}cm")
print(f"最大身長：{max_height}cm")
print(f"最小身長：{min_height}cm")
print(f"身長の範囲：{range_height}cm")

# ヒストグラムで分布を可視化
plt.figure(figsize=(10, 6))
plt.hist(heights, bins=5, edgecolor='black')
plt.title('クラスの身長分布')
plt.xlabel('身長 (cm)')
plt.ylabel('人数')
plt.grid(True, alpha=0.3)
plt.show()

このコードを実行すると、次のような結果が得られます。

平均身長：168.8cm
最大身長：175cm
最小身長：163cm
身長の範囲：12cm

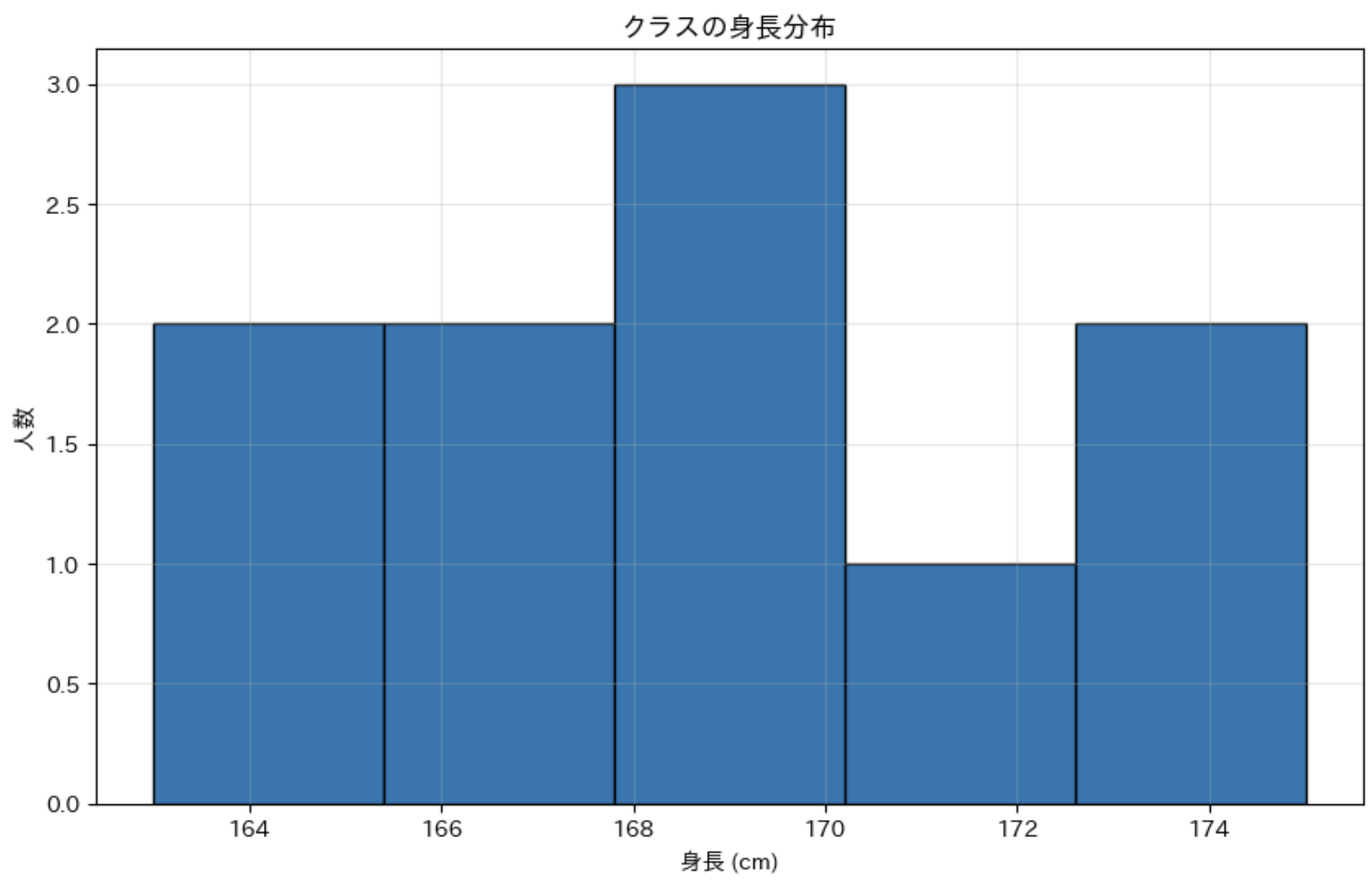
クラスの身長分布

ヒストグラム（度数分布図）によって、身長の分布状況を視覚的に確認することができます。

ヒストグラム: データを一定の区間に分け、その区間に含まれるデータの個数（度数）を棒グラフで表したものです。

テストの点数データの分析

次に、テストの点数データを例に分析をしてみましょう。100 人分の数学のテスト結果があるとします。

テストの点数データ分析

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# 数学テストの点数 (0 から 100 までの整数を、ランダムに 100 個生成)
math_scores = np.random.randint(0, 100, 100)

# 基本統計量の計算
mean_score = np.mean(math_scores)      # 平均点
median_score = np.median(math_scores)  # 中央値
std_score = np.std(math_scores)        # 標準偏差
min_score = np.min(math_scores)        # 最低点
max_score = np.max(math_scores)        # 最高点

print(f"平均点：{mean_score:.1f}")
print(f"中央値：{median_score}")
print(f"標準偏差：{std_score:.1f}")
print(f"最低点：{min_score}")
print(f"最高点：{max_score}")

# ヒストグラムの作成
plt.figure(figsize=(10, 6))
plt.hist(math_scores, bins=10, color='skyblue', edgecolor='black')
# 平均点を示す垂直線を追加
plt.axvline(mean_score, color='red', linestyle='dashed', linewidth=1, label=f'平均点：{mean_score:.1f}')
plt.title('数学テストの点数分布')
plt.xlabel('点数')
plt.ylabel('人数')
# 凡例を表示
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

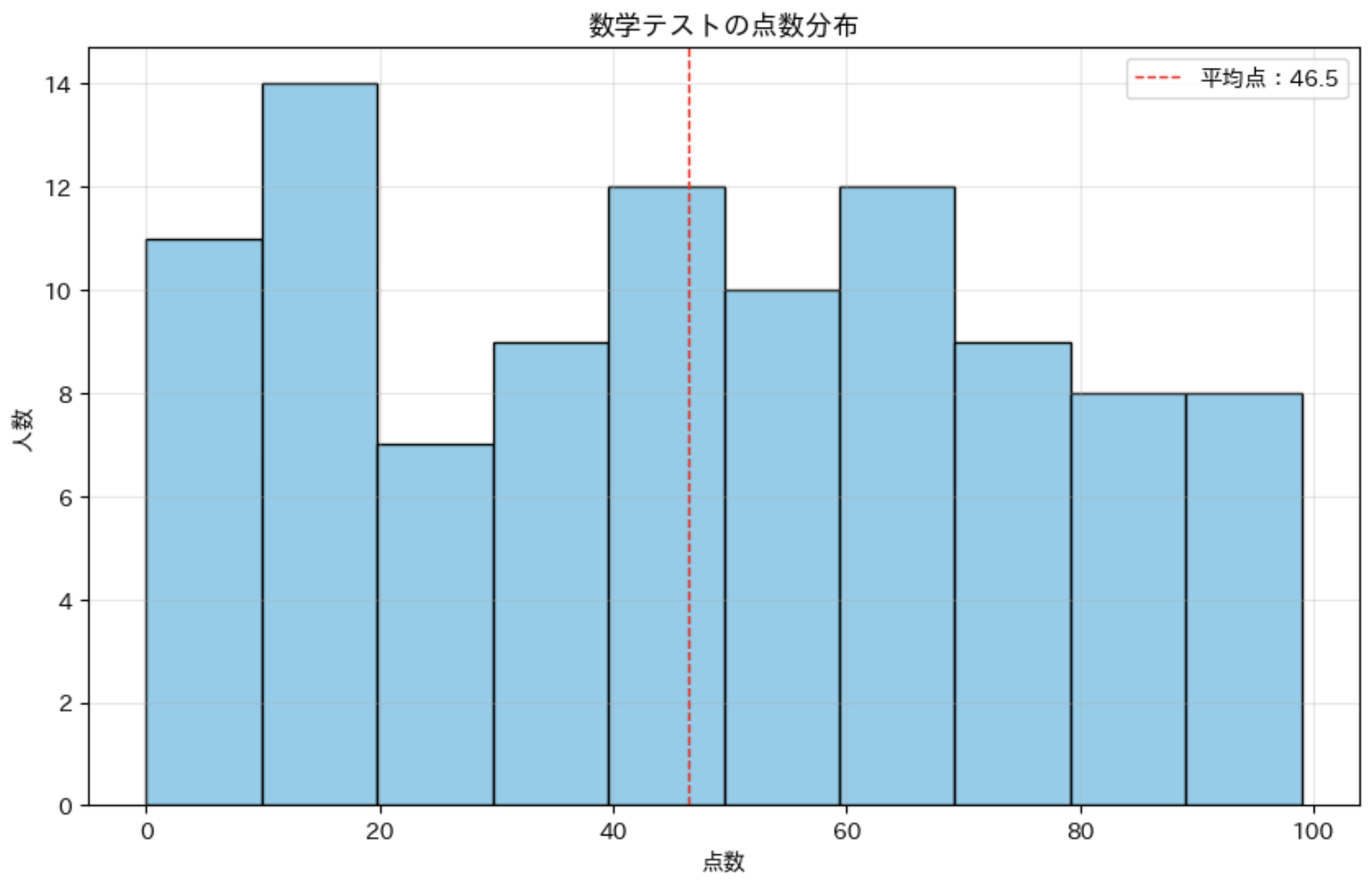
数学テストの点数分布

このコードでは、テストの点数の基本統計量を計算し、ヒストグラムで点数の分布を可視化しています。さらに、ヒストグラム上に平均点を示す垂直線も追加しています。

右上の「平均点：46.5」のようなラベルを凡例と呼びます。

凡例: グラフの各要素に対する説明や注釈を示すものです。これがあることで、特に複数のグラフを一つの図に描画する場合に、どのグラフの値なのかが分かりやすくなります。

9.2 平均・中央値・最頻値でデータの「中心」をつかむ

データの集合から「代表的な値」を一つ選ぶとしたら、どの値を選ぶでしょう？

多くの場合、その集団の「真ん中」あるいは「中心」に近い値を選びたいと思うでしょう。そのような「データの中心傾向」を表す指標として、以下の 3 つがよく使われます：

平均値（Mean）：すべての値の合計をデータ数で割った値
中央値（Median）：データを小さい順に並べた時の中央の値（※1）
最頻値（Mode）：データの中で最も頻繁に現れる値

※1: データ数が奇数の場合は中央の値、偶数の場合は中央の 2 つの値の平均

これらは「代表値」と呼ばれ、それぞれ異なる特性を持っています。

テスト点数データで 3 つの代表値を計算してみよう

具体例として、あるクラスのテスト点数データを使って、3 つの代表値を計算してみましょう。

テストの点数データ

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# 100 個のランダムなテスト点数データを生成 （正規分布に従う）
np.random.seed(42)
# 平均 85, 標準偏差 7 の正規分布から生成し, 60 〜 100 の範囲に制限
scores = np.random.normal(85, 7, 100).clip(60, 100).round().astype(int)

mean_score = np.mean(scores)      # 平均値
median_score = np.median(scores)  # 中央値
# 最頻値を計算
values, counts = np.unique(scores, return_counts=True)
mode_score = values[np.argmax(counts)]

print(f"平均点：{mean_score:.1f}")
print(f"中央値：{median_score}")
print(f"最頻値：{mode_score}")

# ヒストグラムの作成
plt.figure(figsize=(12, 7))
plt.hist(scores, bins=range(60, 101, 5), edgecolor='black', alpha=0.7)

# 3 つの代表値を垂直線で表示
plt.axvline(mean_score, color='red', linestyle='--', linewidth=2, label=f'平均値: {mean_score:.1f}')
plt.axvline(median_score, color='green', linestyle='-.', linewidth=2, label=f'中央値: {median_score}')
plt.axvline(mode_score, color='blue', linestyle=':', linewidth=2, label=f'最頻値: {mode_score}')

plt.title('100 人のテスト点数の分布と 3 つの代表値')
plt.xlabel('点数')
plt.ylabel('人数')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

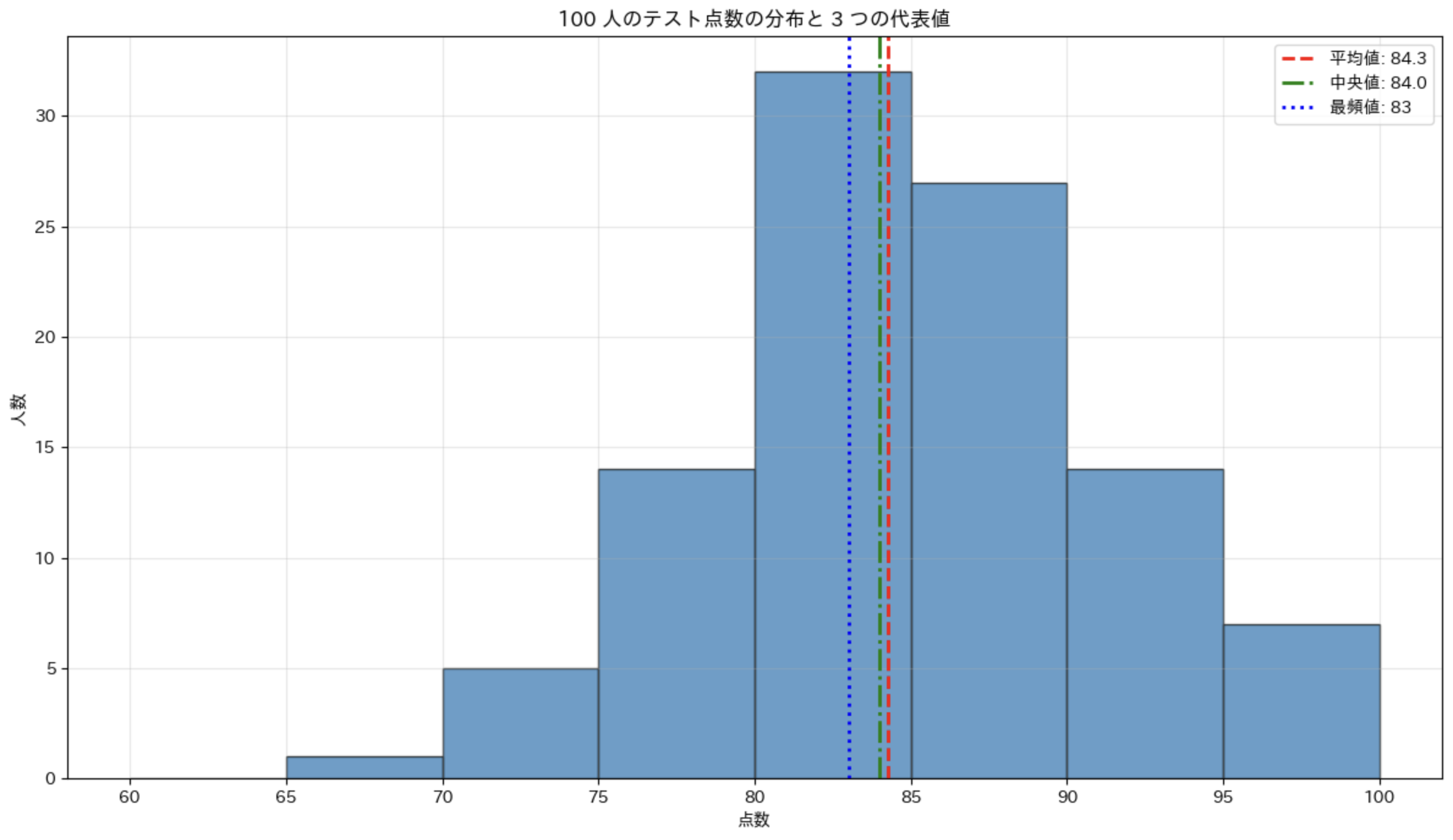
テスト点数の分布と3つの代表値

このデータの場合、3 つの代表値がほぼ同じであることがわかります。これは、このデータが比較的均等に分布していることを示しています。

3 つの代表値の特徴と使い分け

平均値、中央値、最頻値は、それぞれ異なる特徴を持っており、データの性質に応じて使い分けると良いです。

1. 平均値（Mean）

特徴:

すべてのデータ値を反映する
外れ値（極端に大きいまたは小さい値）の影響を受けやすい
連続的な数値データに適している

計算方法:

全てのデータの合計値を、データの個数で割ります。

\bar{x} = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{1}{n} \sum_{i=1}^{n} x_i

適した状況:

データが正規分布に近い場合
外れ値がない、または少ない場合
全体的な傾向を知りたい場合

例：クラスの平均点、平均身長など

2. 中央値（Median）

特徴:

データを順に並べた時の真ん中の値（データ数が偶数の場合は真ん中の2つの平均）
外れ値の影響を受けにくい（ロバスト性がある）
データの分布が歪んでいる場合に有効

計算方法:

データを小さい順に並べる
データ数が奇数なら中央の値、偶数なら中央の 2 つの平均

例：10 人のテスト点数データの中央値は、5 番目と 6 番目の平均値です。

適した状況:

外れ値が存在する場合
データの分布が偏っている場合
順序付けできるデータ（順序尺度以上）

例：所得の中央値、住宅価格の中央値など

3. 最頻値（Mode）

特徴:

データの中で最も頻繁に現れる値
カテゴリカルデータ（質的データ）にも使える
複数存在する可能性がある（多峰性。山が複数ある）

計算方法:

各値の出現回数を数え、最も多く出現する値を選ぶ

適した状況:

カテゴリカルデータの分析
最も「一般的な」値を知りたい場合
離散的な（飛び飛びになった）データの場合

例：人気のある商品、最も多い血液型など

9.3 四分位数と箱ひげ図でデータの広がりを見る

データの特徴を理解するためには、中心だけでなく「どのように広がっているか（分布）」も重要です。

四分位数とは？

四分位数とは、データを小さい順に並べたときに、データを 4 等分する 3 つの値のことです。

第 1 四分位数（ $Q_1$ ）: データの下位 25% の位置にある値
第 2 四分位数（ $Q_2$ ）: データの中央値（50% の位置にある値）
第 3 四分位数（ $Q_3$ ）: データの上位 25% の位置にある値

これらを使って、データの分布の特徴を詳しく知ることができます。四分位範囲は、データのばらつきを表す重要な指標です。

四分位範囲

第 3 四分位数（ $Q_3$ ）と第 1 四分位数（ $Q_1$ ）の差です。

\text{(四分位範囲)} = Q_3 - Q_1

四分位偏差

四分位範囲の半分です。

\text{(四分位偏差)} = \frac{Q_3 - Q_1}{2}

箱ひげ図とは？

箱ひげ図（Box-and-Whisker Plot）は、四分位数を使ってデータの分布を視覚的に表現するためのグラフです。次の要素で構成されています：

箱: $Q_1$ から $Q_3$ までの範囲を表す長方形（箱の中には中央値を示す線が入る）
ひげ: 箱から伸びる線で、通常はデータの最小値と最大値まで伸びる
外れ値: ひげの範囲を超えた値（通常は点でプロット）

箱ひげ図は、データの分布の中心、ばらつき、歪み、外れ値などを一目で把握できるため、非常に便利です。

テストの点数データで箱ひげ図を作ってみよう

箱ひげ図の作成

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# テストの点数データ
test_scores = [65, 70, 75, 78, 80, 82, 85, 88, 90, 92, 95]

# 箱ひげ図の作成
plt.figure(figsize=(10, 6))
plt.boxplot(test_scores, vert=False, patch_artist=True,
            boxprops=dict(facecolor='lightblue'))

# 四分位数を計算して表示
q1 = np.percentile(test_scores, 25)
q2 = np.percentile(test_scores, 50)
q3 = np.percentile(test_scores, 75)
iqr = q3 - q1

print(f"第1四分位数（Q1）：{q1}")
print(f"中央値（Q2）：{q2}")
print(f"第3四分位数（Q3）：{q3}")
print(f"四分位範囲（IQR）：{iqr}")

# 箱ひげ図に統計情報を追加
plt.title('テスト点数の箱ひげ図')
plt.xlabel('点数')
plt.yticks([1], ['テスト点数'])  # y軸のラベル

# 四分位数の位置に垂直線を追加
plt.axvline(q1, color='green', linestyle='--', alpha=0.5)
plt.axvline(q2, color='red', linestyle='--', alpha=0.5)
plt.axvline(q3, color='blue', linestyle='--', alpha=0.5)

# 統計情報をテキストで表示
plt.text(q1, 1.2, f'Q1: {q1}', color='green', ha='center')
plt.text(q2, 1.2, f'Q2: {q2}', color='red', ha='center')
plt.text(q3, 1.2, f'Q3: {q3}', color='blue', ha='center')
plt.text((q1 + q3) / 2, 1.3, f'四分位範囲: {iqr}', ha='center', bbox=dict(facecolor='white', alpha=0.5))

plt.grid(True, axis='x')
plt.tight_layout()
plt.show()

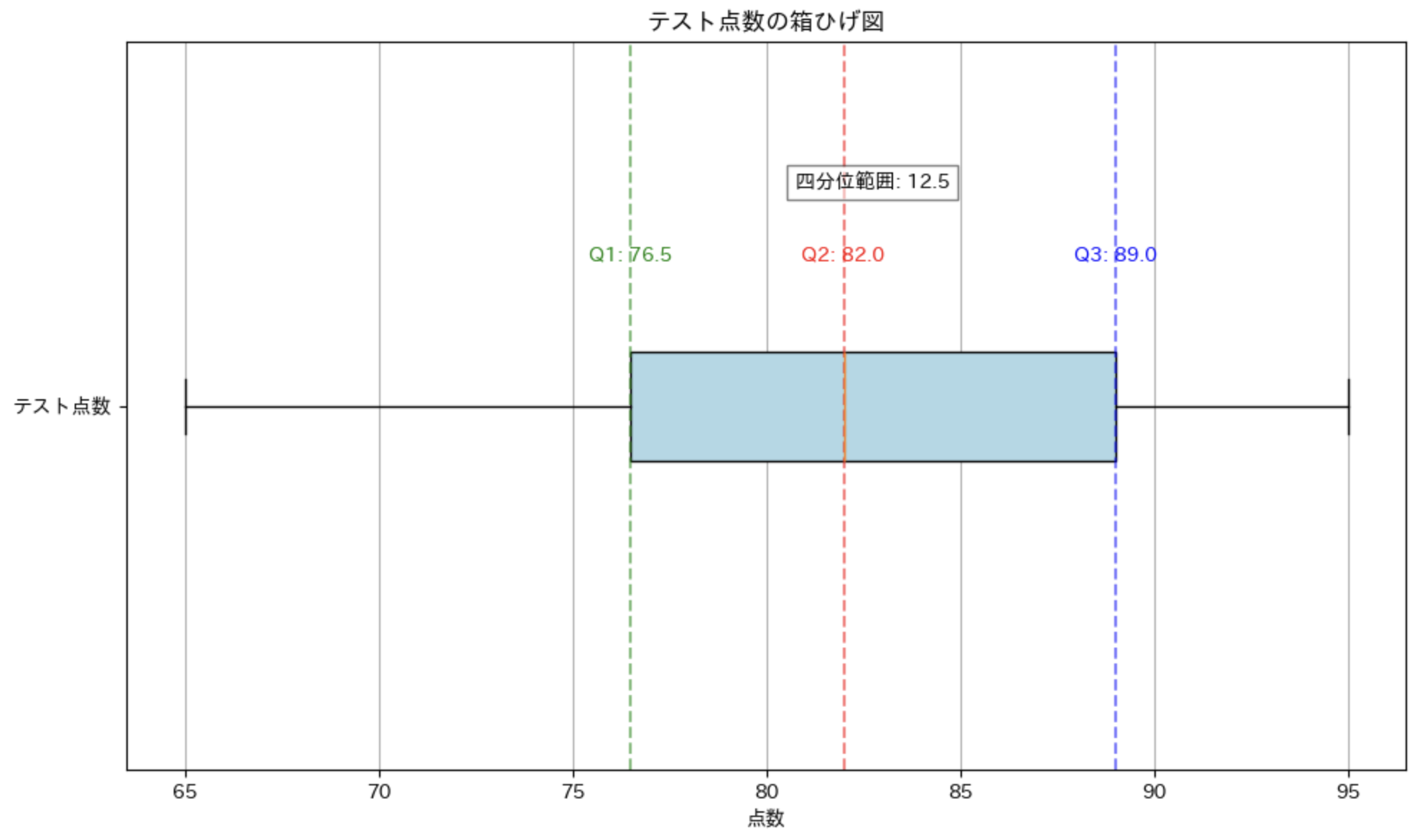
テスト点数の箱ひげ図

外れ値の検出

箱ひげ図は外れ値（異常値）を検出するのにも役立ちます。一般的に、次の基準で外れ値を定義することが多いです：

下側の外れ値: $Q_1 - 1.5 \times \text{IQR}$ より小さい値
上側の外れ値: $Q_3 + 1.5 \times \text{IQR}$ より大きい値

※ IQR は四分位範囲のことです。

これらの値は、箱ひげ図のひげの最大長さを決める基準としてもよく使われます。

外れ値の検出

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# テストの点数データ （外れ値: 55 を含む）
test_scores = [55, 70, 75, 78, 80, 82, 85, 88, 90, 92, 95, 98]

# 箱ひげ図の作成（外れ値も表示）
plt.figure(figsize=(10, 6))
plt.boxplot(
    test_scores,
    vert=False,
    patch_artist=True,
    boxprops=dict(facecolor='lightblue')
)

# 四分位数の計算
q1 = np.percentile(test_scores, 25)
q2 = np.percentile(test_scores, 50)
q3 = np.percentile(test_scores, 75)
iqr = q3 - q1

# 外れ値の基準
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# 外れ値を検出
outliers = [x for x in test_scores if x < lower_bound or x > upper_bound]

print(f"第1四分位数（Q1）：{q1}")
print(f"中央値（Q2）：{q2}")
print(f"第3四分位数（Q3）：{q3}")
print(f"四分位範囲（IQR）：{iqr}")
print(f"外れ値の基準：{lower_bound} 未満 または {upper_bound} 超過")
print(f"検出された外れ値：{outliers}")

# グラフに外れ値の基準線を追加
plt.axvline(lower_bound, color='red', linestyle=':', label=f'外れ値の基準 ({lower_bound:.1f}, {upper_bound:.1f})')
plt.axvline(upper_bound, color='red', linestyle=':')

plt.title('テスト点数の分布と外れ値の検出')
plt.xlabel('点数')
plt.yticks([1], ['テスト点数'])
plt.legend()
plt.grid(True, axis='x')
plt.tight_layout()
plt.show()

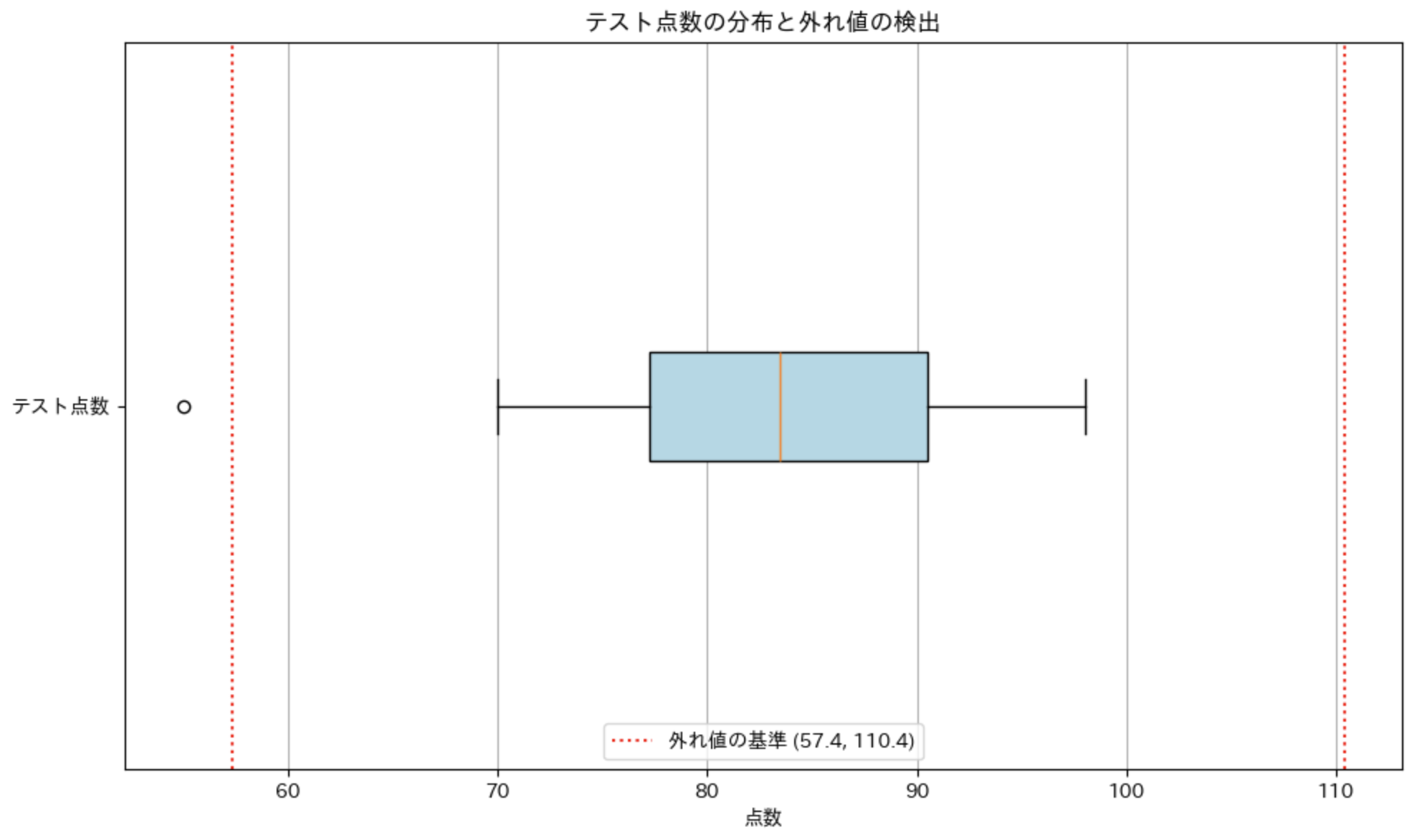
外れ値の検出

9.4 分散・標準偏差でデータのばらつきを数値化

データを分析する上で、中心傾向（平均値や中央値）を知ることは重要ですが、他にも重要な指標があります。

例えば、2 つのクラスの平均点が同じ 80 点だとしても、一方のクラスは全員が 78〜82 点に集中しているのに対し、もう一方のクラスは 60〜100 点まで広く分布している可能性があります。

このような「データの散らばり具合」を数値化するのが、分散と標準偏差です。

分散とは？

分散（Variance）は、データが平均値からどれだけ離れているかを表す指標です。具体的には、各データ点と平均値との差（偏差）の二乗の平均として計算されます。

\text{(分散)} = \frac{1} {n}\sum_{(i = 1)}^{n}(x_i - \bar{x})^2

ここで、 $x_i$ は各データ値、 $\bar{x}$ は平均値、 $n$ はデータの数です。

$(\bar{x} - x_i)$ は、平均値と各データ値との差で、偏差と呼ばれます。

偏差の二乗は、正の値になるため、分散は常に正の値になります。

二乗するのは、偏差が正の値と負の値が打ち消し合うことを防ぐためです。絶対値でないのは、微分して分析するときに都合が良いためです。

分散は言葉で言うと、「偏差平方の平均」です。

標準偏差とは？

標準偏差（Standard Deviation）は、分散の平方根です。

分散は元のデータの単位を二乗した単位になるため、スケールが大きくなりすぎて解釈が難しいという欠点があります。例えば、年収は数 100 万円のようなスケールなので、二乗すると数兆のような、ものすごく大きなスケールになってしまいます。

そこで、分散の平方根を取ることで、元のデータと同じ単位に戻したものが標準偏差です。

例えば、年収データの平均が 500 万円で分散が 10,000,000,000（1 兆）だとすると、このままでは解釈が難しいですが、標準偏差は 100 万円となり、「データは平均から概ね ±100 万円の範囲に分布している」と直感的に理解できます。

\text{(標準偏差)} = \sqrt{\text{(分散)}} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2}

2つのクラスの点数データで比較してみよう

分散と標準偏差の概念を理解するために、ばらつきの異なる2つのクラスのテスト点数データを比較してみましょう。

テストの点数データ

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# 2 つのクラスの点数データ
class_a = [82, 85, 88, 84, 87, 83, 86, 85, 84, 86]  # ばらつきが小さい
class_b = [65, 95, 75, 90, 85, 70, 95, 65, 80, 85]  # ばらつきが大きい

# 分析関数の定義
def analyze_scores(scores, class_name):
    mean = np.mean(scores)  # 平均
    var = np.var(scores)    # 分散
    std = np.std(scores)    # 標準偏差

    print(f"\n{class_name}の分析:")
    print(f"平均点：{mean:.1f}")
    print(f"分散：{var:.1f}")
    print(f"標準偏差：{std:.1f}")

    return mean, std

# 2 つのクラスを分析
mean_a, std_a = analyze_scores(class_a, "クラスA")
mean_b, std_b = analyze_scores(class_b, "クラスB")

# ヒストグラムで比較
plt.figure(figsize=(12, 5))

# クラス A のヒストグラム
plt.subplot(1, 2, 1)
plt.hist(class_a, bins=5, edgecolor='black', alpha=0.7)
plt.title('クラスAの点数分布（ばらつき小）')
plt.xlabel('点数')
plt.ylabel('人数')
plt.xlim(60, 100)
plt.axvline(mean_a, color='red', linestyle='--', label=f'平均: {mean_a:.1f}')
plt.axvline(mean_a + std_a, color='green', linestyle=':', label=f'標準偏差: {std_a:.1f}')
plt.axvline(mean_a - std_a, color='green', linestyle=':')
plt.legend()

# クラス B のヒストグラム
plt.subplot(1, 2, 2)
plt.hist(class_b, bins=5, edgecolor='black', alpha=0.7)
plt.title('クラスBの点数分布（ばらつき大）')
plt.xlabel('点数')
plt.xlim(60, 100)
plt.axvline(mean_b, color='red', linestyle='--', label=f'平均: {mean_b:.1f}')
plt.axvline(mean_b + std_b, color='green', linestyle=':', label=f'標準偏差: {std_b:.1f}')
plt.axvline(mean_b - std_b, color='green', linestyle=':')
plt.legend()

plt.tight_layout()
plt.show()

このコードを実行すると、以下のような結果が得られます。

クラスAの分析:
平均点：85.0
分散：3.0
標準偏差：1.7

クラスBの分析:
平均点：80.5
分散：117.2
標準偏差：10.8

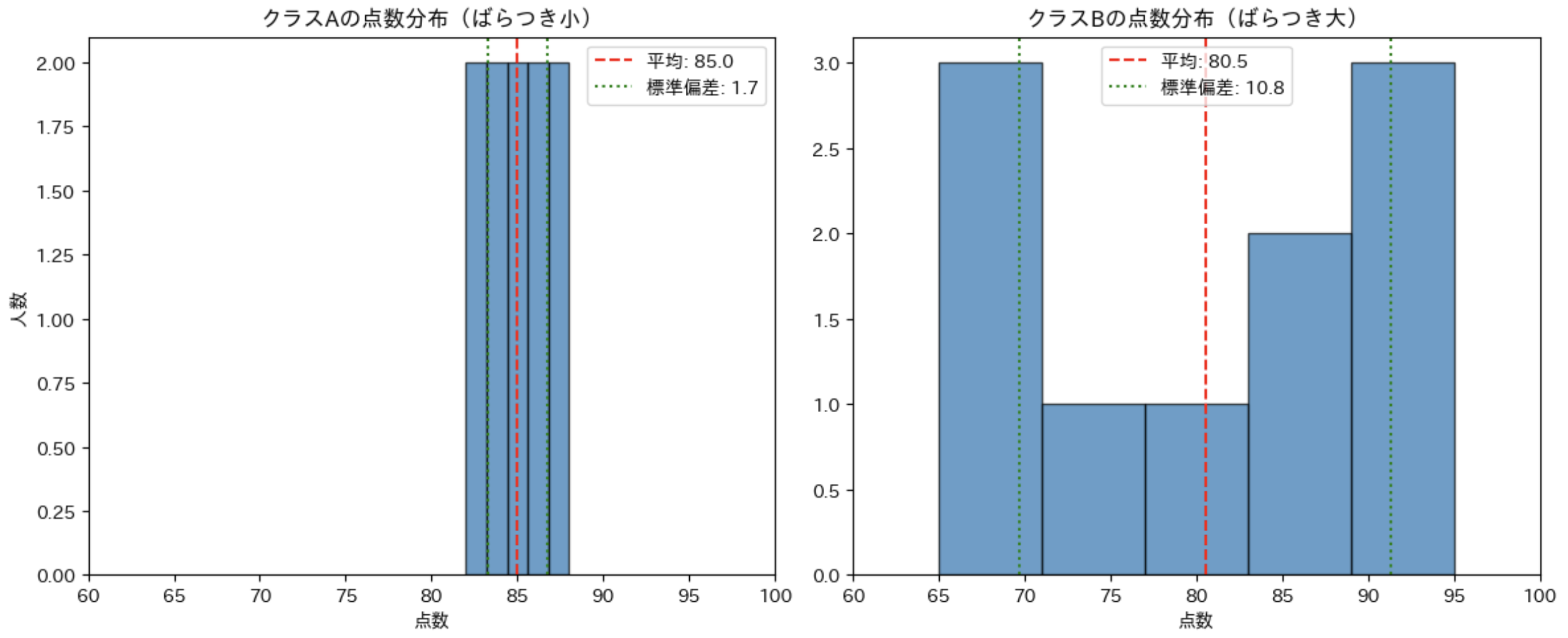
2つのクラスの点数データ

たしかに、クラス B の標準偏差は大きい値になっています。

9.5 散布図で 2 つのデータの関係を調べよう

2 つの要素の間に関係があるかどうかを知りたい場面が多くあります。例えば、

数学の点数と理科の点数の関係
運動量と体重減少の関係
商品の価格と売上数の関係

こうした 2 つの変数の関係を視覚的に表現するのに最適なのが「散布図」です。

散布図とは？

散布図（Scatter Plot）は、2つの変数のデータをx-y平面上の点としてプロットしたグラフです。各点は (x, y) 座標で表され、x 軸が一方の変数、y 軸がもう一方の変数を表します。

色々な例を見てみましょう。

様々な相関パターン

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib


# 乱数の種を固定 （再現性のため）
np.random.seed(42)

# 4 つの異なるパターンのデータを生成
n = 50  # データ点の数

# 1. 強い正の相関
x1 = np.linspace(0, 10, n)
y1 = 2 * x1 + 5 + np.random.normal(0, 1, n)

# 2. 強い負の相関
x2 = np.linspace(0, 10, n)
y2 = 20 - 1.5 * x2 + np.random.normal(0, 1, n)

# 3. 相関なし
x3 = np.linspace(0, 10, n)
y3 = np.random.normal(10, 3, n)

# 4. 非線形の関係
x4 = np.linspace(0, 10, n)
y4 = 2 * (x4 - 5)**2 + np.random.normal(0, 3, n)

# 4つのサブプロットを作成
plt.figure(figsize=(12, 10))

# 強い正の相関
plt.subplot(2, 2, 1)
plt.scatter(x1, y1, color='blue', alpha=0.7)
plt.title('強い正の相関')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True, alpha=0.3)

# 強い負の相関
plt.subplot(2, 2, 2)
plt.scatter(x2, y2, color='red', alpha=0.7)
plt.title('強い負の相関')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True, alpha=0.3)

# 相関なし
plt.subplot(2, 2, 3)
plt.scatter(x3, y3, color='green', alpha=0.7)
plt.title('相関なし')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True, alpha=0.3)

# 非線形の関係
plt.subplot(2, 2, 4)
plt.scatter(x4, y4, color='purple', alpha=0.7)
plt.title('非線形の関係')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

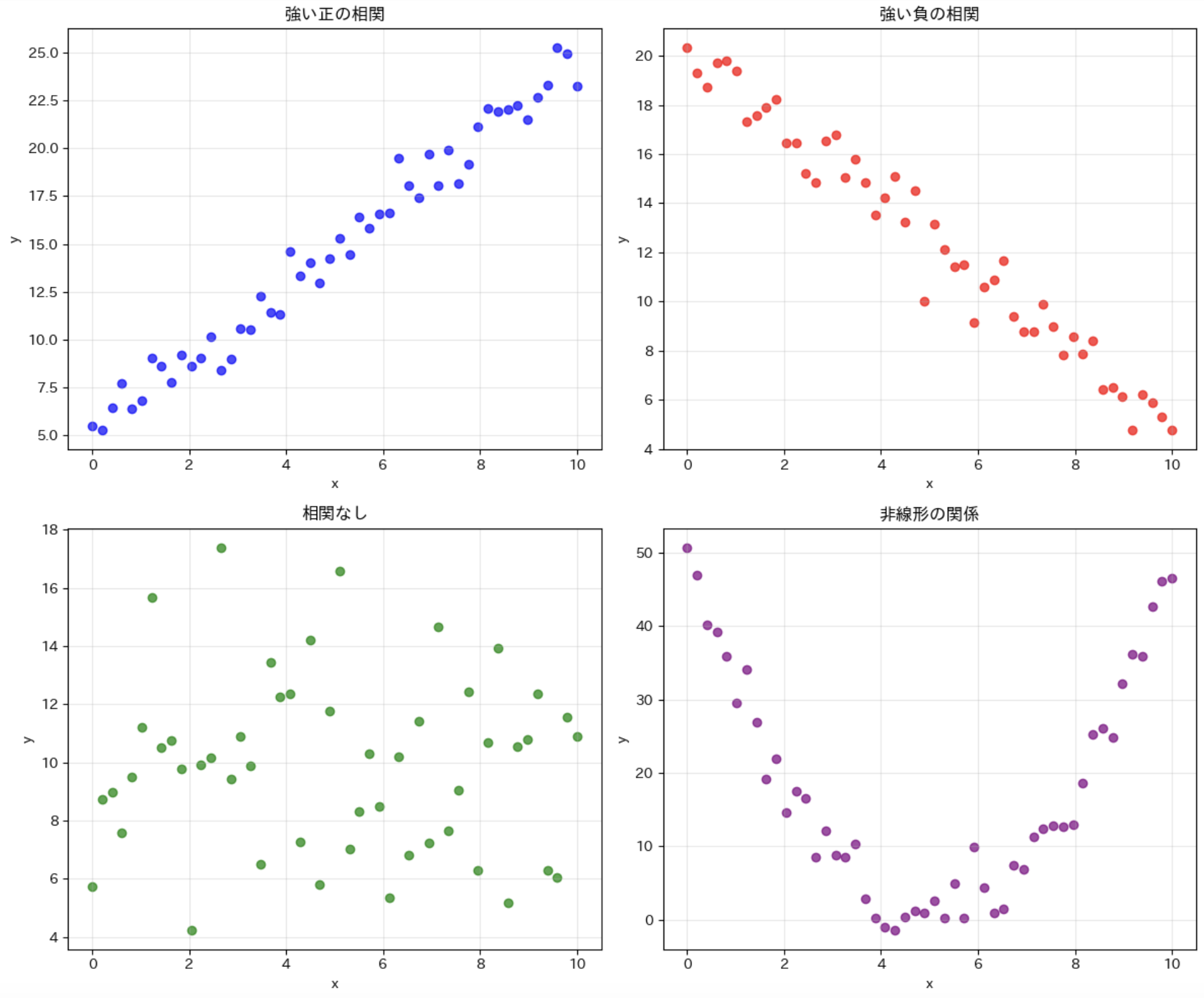
様々な相関パターン

このコードでは、4 つの異なる関係性のパターンを持つデータを生成し、それぞれの散布図を表示しています。

強い正の相関：x が増加すると y も増加する
強い負の相関：x が増加すると y は減少する
相関なし：x と y の間に明確な関係がない
非線形の関係：x と y の間に関係はあるが、直線的ではない

9.6 相関係数で「強い関係」か「弱い関係」か判断する

視覚的な判断だけだと、主観的になりがちです。2 つの変数の関係の強さを数値で表す「相関係数」について学びましょう。まずは、共分散と相関係数の定義を確認します。

共分散とは？

共分散（Covariance）は、2 つの変数の間の関係の強さを測る統計指標です。これは、2 つの変数の偏差の積の平均値です。

\text{(共分散)} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})

分散では、偏差を二乗していました。共分散では、x の偏差と y の偏差をそのまま掛け合わせています。

そのため、共分散は正の値も負の値も取り得るので注意しましょう。

相関係数とは？

相関係数（Correlation Coefficient）は、2つの変数の間の関係の強さと方向を測る統計指標です。これは線形関係の強さを -1 から +1 の間の値で表します。

+1：完全な正の相関（一方が増加すると、もう一方も増加。一直線上に並ぶ）
0：相関なし（2 つの変数の間に線形関係がない）
-1：完全な負の相関（一方が増加すると、もう一方は減少。一直線上に並ぶ）

相関係数の絶対値が大きいほど、相関関係が強いことを示します。

r = \frac{\text{(x と y の共分散)}}{\text{(x の標準偏差)} \times \text{(y の標準偏差)}}

数式（記号や数値）で書くと、以下のようになります。

r = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}

$\frac{1}{n}$ がキャンセル（約分）されていることが分かります。また、スケールも標準化されているので、相関係数は -1 から 1 の間の値になります。

相関関係があるからといって、因果関係があるとは限らないので注意しましょう。第三の変数が影響している可能性があります。また、因果関係の方向が逆だったり、そもそも偶然である可能性もあります。

例えば、「朝食をとる生徒は成績が良い傾向がある」は、「朝食をとることが脳に良い」という可能性もありますが、「そもそも規則正しい生活を送っているので、勉強習慣もあって成績も良い」という可能性もあります。

色々な値の相関関係のグラフ

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats


# フォントサイズの設定
plt.rcParams['font.size'] = 12

# 相関係数のリスト
correlations = [0.9, 0.7, 0.5, 0.3, 0.0, -0.3, -0.5, -0.7, -0.9]

# サブプロットの設定
fig, axes = plt.subplots(3, 3, figsize=(15, 15))
axes = axes.flatten()

# 各相関係数についてデータを生成し、散布図と回帰直線を描画
for i, corr in enumerate(correlations):
    # データ数
    n = 100

    # 相関係数からデータを生成する
    mean = [0, 0]
    cov = [[1, corr], [corr, 1]]
    x, y = np.random.multivariate_normal(mean, cov, n).T

    # 散布図の描画
    axes[i].scatter(x, y, alpha=0.7)

    # 回帰直線の描画
    slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
    x_line = np.linspace(min(x), max(x), 100)
    y_line = slope * x_line + intercept
    axes[i].plot(x_line, y_line, 'r-', linewidth=2)

    # 相関係数の表示（計算された実際の値）
    title = f'相関係数 = {r_value:.2f}'
    axes[i].set_title(title)
    axes[i].set_xlabel('X変数')
    axes[i].set_ylabel('Y変数')

    # 軸の範囲を統一
    axes[i].set_xlim(-3, 3)
    axes[i].set_ylim(-3, 3)

    # グリッド表示
    axes[i].grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.savefig('correlation_examples.png', dpi=300)
plt.show()

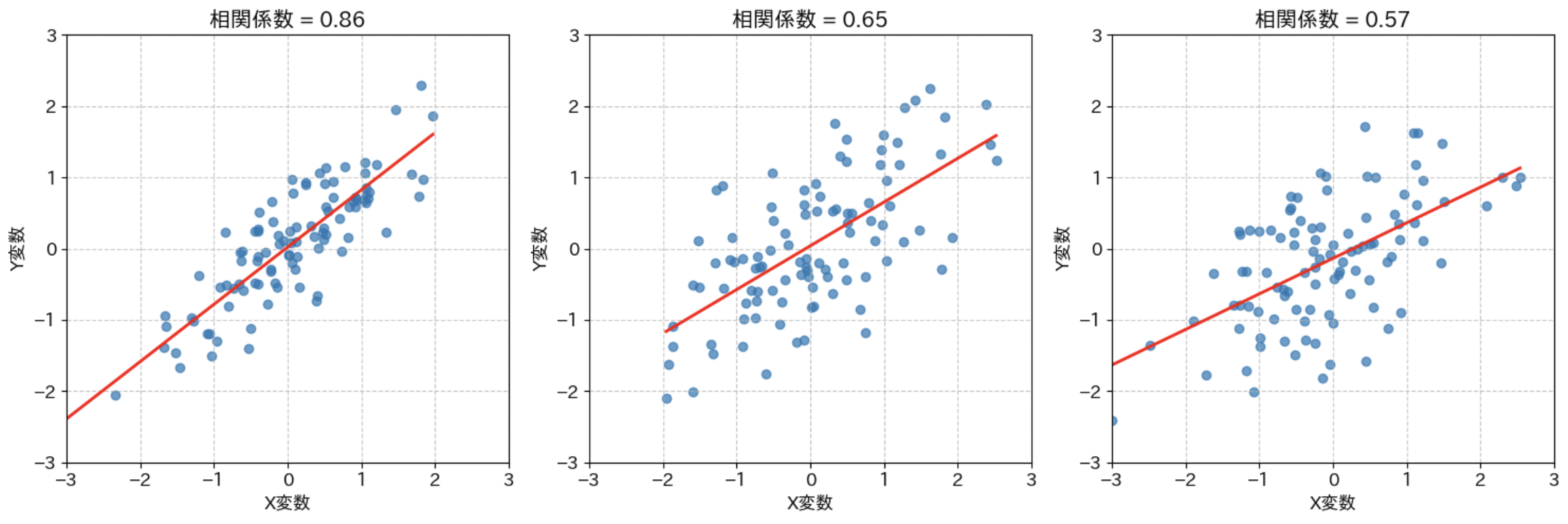
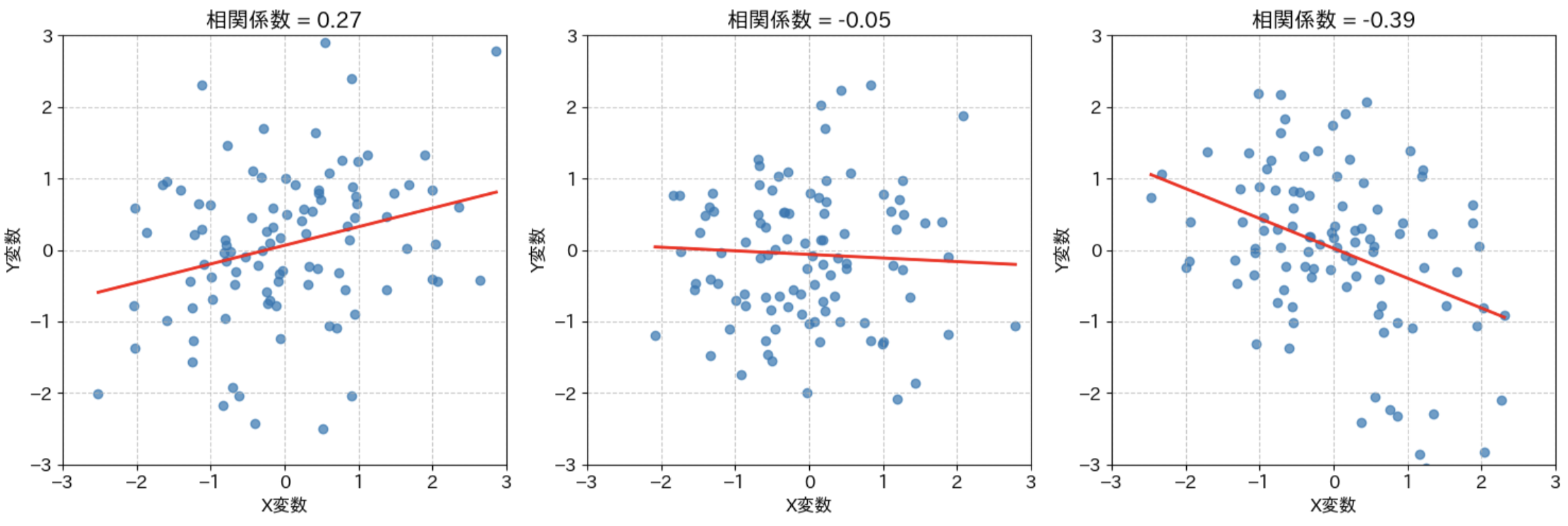
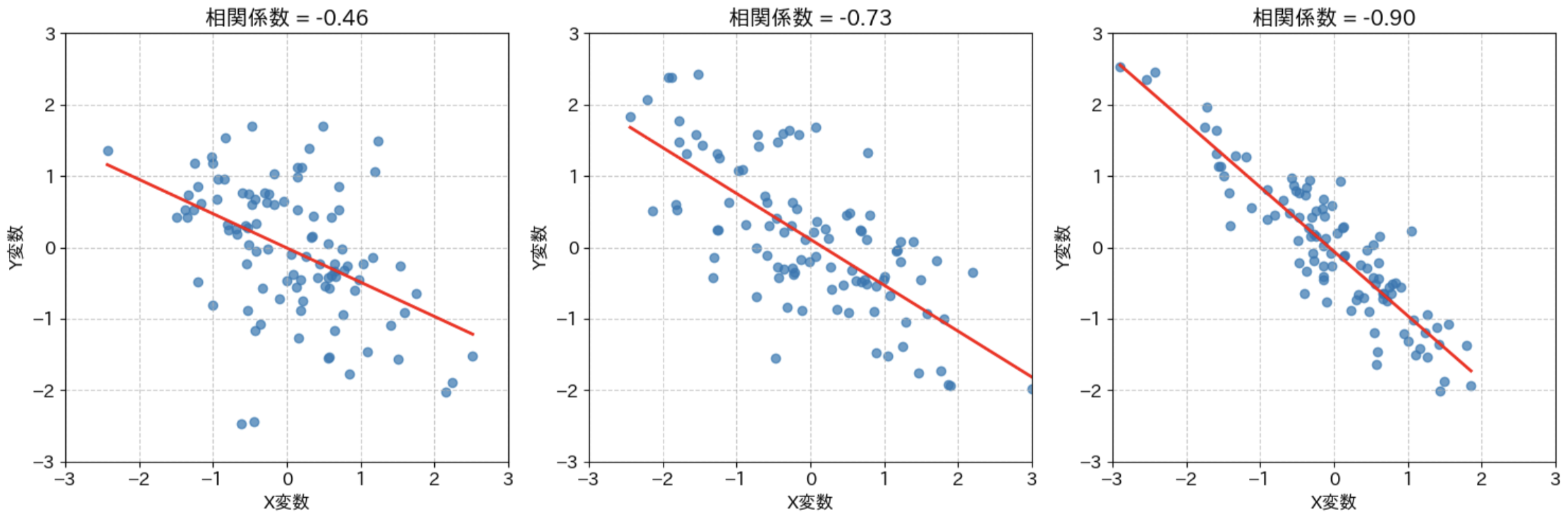
色々な値の相関関係のグラフ

このように、実際のグラフを見てみるとイメージしやすいです。

相関係数の絶対値は、どのくらい直線にフィットしているかを表します。傾き自体は値に関係ないので注意しましょう（プラスかマイナスかだけです）。

9.7 回帰直線で「未来」を予測してみる

回帰分析（Regression Analysis）は、一つ以上の説明変数と目的変数の間の関係をモデル化し、そのモデルを使って新しいデータの値を予測する統計的手法です。

言葉で言うと難しそうなので、実際の例を見てみましょう。

回帰直線の考え方

単回帰分析では、データに最もフィットする直線（回帰直線）を見つけます。回帰直線の式は以下の形で表されます。

y = ax + b

$y$ は目的変数（予測したい値）, $x$ は説明変数（既知の値）, $a$ は直線の傾き（回帰係数）, $b$ は切片です。

回帰直線は、実データの点からの「誤差の二乗和」が最小になるように計算されます。この方法は「最小二乗法」と呼ばれます。

勉強時間とテスト点数の回帰分析

勉強時間からテスト点数を予測する例で回帰分析を行ってみましょう。

回帰分析の基本

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.linear_model import LinearRegression
from scipy.stats import pearsonr

# シード値を設定して再現性を確保
np.random.seed(42)
n = 100  # データ数
x_mean = 3  # x 軸の平均値
x_std = 1   # x 軸の標準偏差
slope = 8   # 実際の傾き
intercept = 60  # 実際の切片
noise_level = 10  # ノイズレベル （大きいほど相関係数が小さくなる）

# 勉強時間のデータを生成 （正規分布に従う）
study_hours = np.random.normal(loc=x_mean, scale=x_std, size=n)
study_hours = np.clip(study_hours, 0, 6)  # 現実的な範囲に収める (0 〜 6 時間)

# ノイズを加えてテスト点数を生成
noise = np.random.normal(loc=0, scale=noise_level, size=n)
test_scores = slope * study_hours + intercept + noise
test_scores = np.clip(test_scores, 40, 100)  # 現実的な点数範囲に収める (40 〜 100 点)

# 相関係数を計算
correlation, _ = pearsonr(study_hours, test_scores)

# 線形回帰モデルの作成
X = study_hours.reshape(-1, 1)  # 形状を変換
model = LinearRegression()
model.fit(X, test_scores)  # モデルの学習

# モデルの係数 （傾きと切片）
slope_fitted = model.coef_[0]
intercept_fitted = model.intercept_

# 散布図と回帰直線の可視化
plt.figure(figsize=(12, 8))
plt.scatter(study_hours, test_scores, color='blue', s=70, alpha=0.6, label='実データ')

# 回帰直線
x_range = np.linspace(0, 6, 100).reshape(-1, 1)
y_pred = model.predict(x_range)
plt.plot(x_range, y_pred, 'r-', linewidth=2, label=f'回帰直線: y = {slope_fitted:.2f}x + {intercept_fitted:.2f}')

# グラフの装飾
plt.title(f'勉強時間とテスト点数の回帰分析 (相関係数: {correlation:.2f})', fontsize=16)
plt.xlabel('勉強時間（時間）', fontsize=14)
plt.ylabel('テスト点数', fontsize=14)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(fontsize=12)
plt.xlim(0, 6)
plt.ylim(40, 100)
plt.tight_layout()
plt.show()

# 回帰直線の解釈
print(f"回帰直線: y = {slope_fitted:.2f}x + {intercept_fitted:.2f}")
print(f"解釈: 勉強時間が 1 時間増えると、テスト点数は平均して {slope_fitted:.2f} 点上がる")

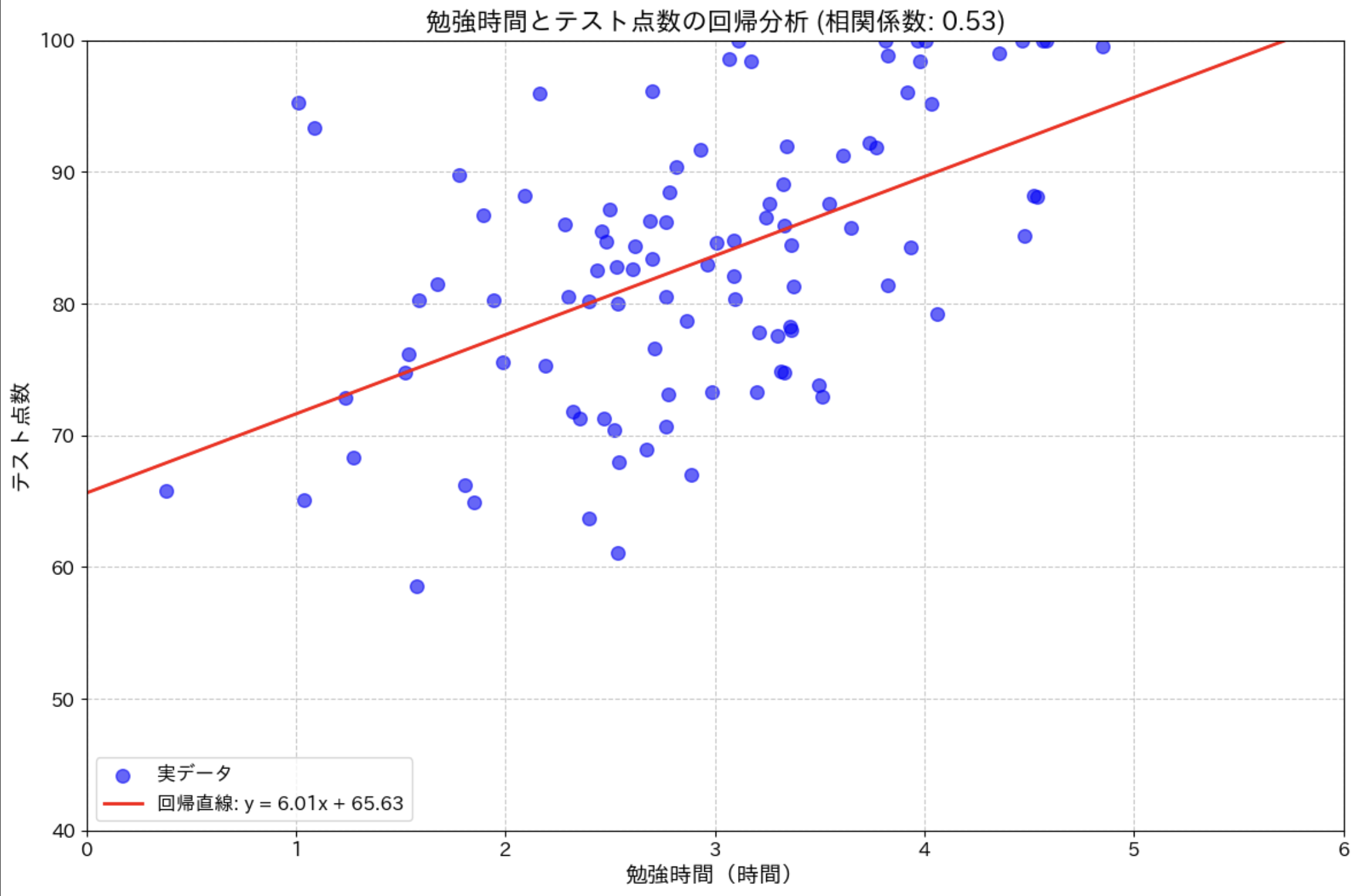
勉強時間とテスト点数の回帰分析

このコードでは、scikit-learn の LinearRegression クラスを使って回帰モデルを作成しています。モデルの学習後、係数（傾きと切片）が得られ、それを使って回帰直線を描画しています。

scikit-learn（サイキットラーン）は、データ分析（特に機械学習）のための Python のライブラリです。回帰分析以外にも、分類やクラスタリングなどの多くの機械学習アルゴリズムを使うことができます。

複数の説明変数を使った予測（重回帰分析）

実際の予測では、一つの変数だけでなく複数の変数を考慮することが多いです。例えば、テスト点数を予測する際に、勉強時間だけでなく睡眠時間も考慮するとより精度が上がるかもしれません。

また、例えば家賃を予測する際に、部屋の広さだけでなく、駅からの距離や築年数も考慮するとより精度が上がるかもしれません。

高校で学習する回帰は、変数が一つの場合の「単回帰分析」ですが、実際には複数の変数を考慮する「重回帰分析」を使うことが多いです。

Ex.1 クラス全員の身長データから平均・中央値・標準偏差を計算して特徴をまとめる

クラス全員の身長データから平均・中央値・標準偏差を計算して特徴をまとめる

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy import stats


def analyze_height_data():
    # 身長データ （cm）
    heights = [
        158, 160, 165, 168, 170, 172, 175, 163, 167, 169,
        164, 166, 171, 173, 168, 167, 165, 170, 172, 169,
    ]

    # 基本統計量の計算
    mean = np.mean(heights)
    median = np.median(heights)
    std = np.std(heights)
    # 最頻値の計算
    mode_result = stats.mode(heights)
    mode = mode_result.mode

    # 結果の表示
    print("身長データの分析結果:")
    print(f"平均値：{mean:.1f}cm")
    print(f"中央値：{median:.1f}cm")
    print(f"最頻値：{mode}cm")
    print(f"標準偏差：{std:.1f}cm")

    # ヒストグラムと正規分布
    plt.figure(figsize=(10, 6))
    plt.hist(heights, bins=10, density=True, alpha=0.7, label='実データ')

    # 正規分布曲線
    x = np.linspace(min(heights), max(heights), 100)
    y = stats.norm.pdf(x, mean, std)
    plt.plot(x, y, 'r-', label='正規分布')

    plt.title('クラスの身長分布')
    plt.xlabel('身長 (cm)')
    plt.ylabel('頻度')
    plt.legend()
    plt.grid(True)
    plt.show()


analyze_height_data()

チャレンジ：

男女別のデータに分けて比較分析してみよう
箱ひげ図（ボックスプロット）も描画して外れ値を確認してみよう
全国平均（データを調べて持ってくる）と比較して、このクラスの特徴を考察してみよう

Ex.2 勉強時間とテスト点数のデータで散布図を描き、相関係数や回帰直線を求めて関係を考える

勉強時間とテスト点数のデータで散布図を描き、相関係数や回帰直線を求めて関係を考える

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.linear_model import LinearRegression


def analyze_study_data():
    # 1 週間の勉強時間 （時間） とテスト点数のデータ
    study_hours = np.array([1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 2.0, 2.5, 3.0, 3.5, 4.0, 3.0, 3.5]).reshape(-1, 1)
    test_scores = np.array([65, 70, 75, 80, 85, 90, 95, 68, 72, 78, 82, 88, 77, 83])

    # 相関係数の計算
    correlation = np.corrcoef(study_hours.flatten(), test_scores)[0, 1]
    print(f"相関係数：{correlation:.3f}")

    # 回帰分析
    model = LinearRegression()
    model.fit(study_hours, test_scores)

    # 回帰直線の係数
    slope = model.coef_[0]
    intercept = model.intercept_
    print(f"\n回帰直線: y = {slope:.1f}x + {intercept:.1f}")
    print(f"傾き：{slope:.1f}（1時間勉強時間が増えると点数が{slope:.1f}点上がる）")

    # 予測例
    study_time = 5.0
    predicted_score = model.predict([[study_time]])[0]
    print(f"\n{study_time}時間勉強した場合の予測点数：{predicted_score:.1f}点")

    # グラフの作成
    plt.figure(figsize=(10, 6))

    # 散布図
    plt.scatter(study_hours, test_scores, color='blue', label='実データ', alpha=0.7)

    # 回帰直線
    x_range = np.linspace(1, 5, 100).reshape(-1, 1)
    y_pred = model.predict(x_range)
    plt.plot(x_range, y_pred, 'r--', label=f'回帰直線 (相関係数: {correlation:.3f})')

    # グラフの装飾
    plt.title('勉強時間とテスト点数の関係')
    plt.xlabel('勉強時間（時間）')
    plt.ylabel('テスト点数')
    plt.grid(True, linestyle='--', alpha=0.7)
    plt.legend()
    plt.show()


analyze_study_data()

チャレンジ：

複数教科のデータで同じ分析を行い、教科による違いを比較してみよう
1 週間ごとの勉強パターン（平日と週末の違いなど）と点数の関係を調べてみよう
クラスメイト全員のデータを集めて、全体的な傾向とグループ分けをしてみよう

まとめ

この章で学んだこと：

データの中心を表す3つの指標
- 平均値：全体の代表的な値
- 中央値：データを順に並べた時の中央
- 最頻値：最も多く出現する値
データのばらつきを表す指標
- 分散：データのばらつきの大きさ
- 標準偏差：ばらつきを元のデータと同じ単位で表現
- 四分位数：データを4等分する値
データの関係性を調べる方法
- 散布図：2つの変数の関係を視覚化
- 相関係数：関係の強さを-1から1の数値で表現
- 回帰直線：データの傾向を直線で表現
実践的な活用法
- 成績データの分析
- 身長・体重などの身体測定データの特徴把握
- 学習時間と成績の関係分析
- 将来の予測

次の章では、Python を使った数値シミュレーションを学びます！

9. 身近なデータで学ぶ統計の基本

目次

この講座で使用する Google Colab の URL

演習課題

この講座で使用する Python, Jupyter Notebook のファイルと実行環境

統計で何がわかるのか

NumPy で統計計算をする

身近な例で統計を考えてみよう

クラスの身長データ例

テストの点数データの分析

テストの点数データ分析

テスト点数データで 3 つの代表値を計算してみよう

テストの点数データ

3 つの代表値の特徴と使い分け

1. 平均値（Mean）

2. 中央値（Median）

3. 最頻値（Mode）

四分位数とは？

四分位範囲

四分位偏差

箱ひげ図とは？

テストの点数データで箱ひげ図を作ってみよう

箱ひげ図の作成

外れ値の検出

外れ値の検出

分散とは？

標準偏差とは？

2つのクラスの点数データで比較してみよう

テストの点数データ

散布図とは？

様々な相関パターン

共分散とは？

相関係数とは？

色々な値の相関関係のグラフ

色々な値の相関関係のグラフ

回帰直線の考え方

勉強時間とテスト点数の回帰分析

回帰分析の基本

複数の説明変数を使った予測（重回帰分析）

クラス全員の身長データから平均・中央値・標準偏差を計算して特徴をまとめる

勉強時間とテスト点数のデータで散布図を描き、相関係数や回帰直線を求めて関係を考える

まとめ